Gravitational-wave Searches
What are the targets of Einstein@Home's gravitational-wave search?
Einstein@Home searches for weak, continuous (long-duration) gravitational waves from spinning neutron stars in data from the LIGO detectors.
What are neutron stars?
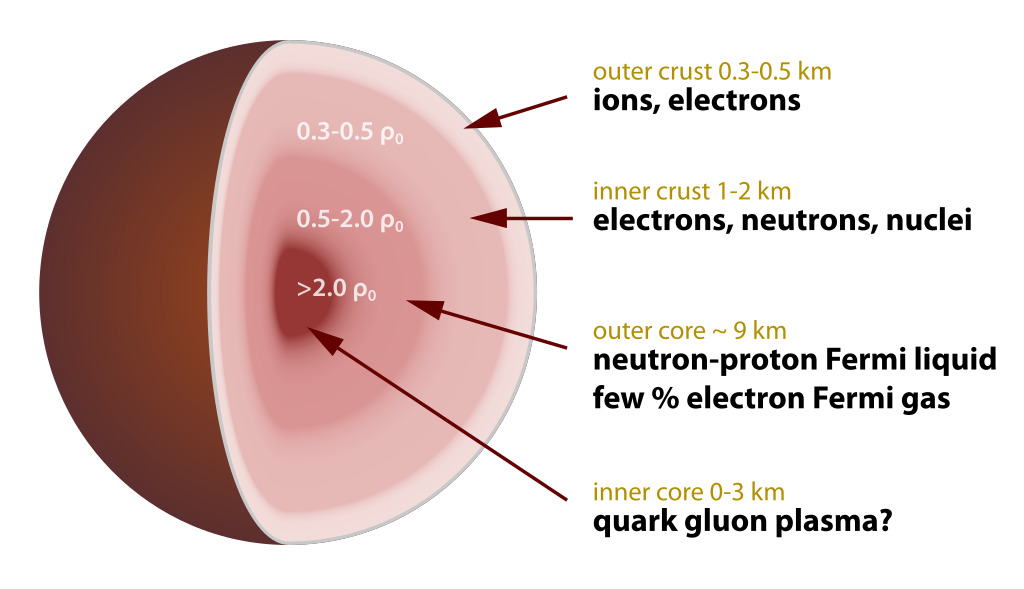 Neutron stars are compact and exotic objects. They have a diameter of between 20 and 30 kilometers – about the size of a small city. At the same time, their mass is on average that of half a million Earths, or 1.4 times that of our Sun. These objects are composed of matter that is much denser than ordinary matter anywhere in the Universe. The density of a neutron star is comparable to that of an atomic nucleus (and possibly even higher inside). Neutron stars have strong magnetic fields, up to a trillion times stronger than a refrigerator magnet. Some also spin around their axis up to hundreds of times per second. The image on the right shows the interior structure of a neutron star.
Neutron stars are compact and exotic objects. They have a diameter of between 20 and 30 kilometers – about the size of a small city. At the same time, their mass is on average that of half a million Earths, or 1.4 times that of our Sun. These objects are composed of matter that is much denser than ordinary matter anywhere in the Universe. The density of a neutron star is comparable to that of an atomic nucleus (and possibly even higher inside). Neutron stars have strong magnetic fields, up to a trillion times stronger than a refrigerator magnet. Some also spin around their axis up to hundreds of times per second. The image on the right shows the interior structure of a neutron star.
How do neutron stars form?
Regular stars (like our Sun) are powered by nuclear fusion, i.e., by combining atomic nuclei of lighter elements into those of heavier elements (and releasing energy during the process). When a star several times the mass of our Sun has used up all of its nuclear fuel, it explodes in an energetic event called a supernova. As the star's core of mostly iron collapses under its own gravity, the outer layers of the star are blasted away. Gravity squeezes the core of the star so hard that the protons and electrons inside combine to form neutrons and neutrinos. The resulting object is called a neutron star.
Do spinning neutron stars emit gravitational waves?
Because of their high density, small size, and strong gravity, at first one might expect neutron stars to be always perfectly spherical. If this were the case, no rotating neutron star could emit gravitational waves: Perfectly round objects do not emit gravitational waves, no matter how fast they spin.
But fortunately, things are not that simple and boring: there are several ways to deform neutron stars non-axisymmetrically (see the next topic for more details). Deformed rotating neutron stars are a source of gravitational waves. As long as the deformation exists, the neutron star will emit gravitational waves at twice its rotational frequency. We know of nearly 3500 rotating neutron stars detected as pulsars in the electromagnetic spectrum. About 20% of them could emit gravitational waves in the frequency band observed by ground-based detectors like LIGO. Looking for their gravitational-wave emission is the only way to find out how deformed they are and to find neutron stars not detectable as pulsars in the electromagnetic spectrum.
Learn more about this topic in this video hosted on YouTube.
How does nature deform a neutron star?
 There are several processes that could lead to deformations of rotating neutron stars. The outside of the neutron star is expected to be a crystalline crust several hundred meters thick. This is not ordinary matter and is 20 times as hard as steel. The crust could therefore support tiny “hills” or small “bumps” on the surface of the neutron star (see image on the right for an artist's impression). These bumps could form during the birth process of the neutron star in the aftermath of the supernova. Alternatively, they could form later when matter from a companion star – guided by the neutron star's strong magnetic field – accretes onto a small part of the neutron star's surface.
There are several processes that could lead to deformations of rotating neutron stars. The outside of the neutron star is expected to be a crystalline crust several hundred meters thick. This is not ordinary matter and is 20 times as hard as steel. The crust could therefore support tiny “hills” or small “bumps” on the surface of the neutron star (see image on the right for an artist's impression). These bumps could form during the birth process of the neutron star in the aftermath of the supernova. Alternatively, they could form later when matter from a companion star – guided by the neutron star's strong magnetic field – accretes onto a small part of the neutron star's surface.
The size of neutron star bumps is expected to be only centimeters. It is usually measured by a quantity called “ellipticity”. It roughly describes how much the neutron star (measured relative to its radius) deviates from a perfect sphere. For typical neutron star crust bumps, the ellipticity can be as “large” as 10-6. This is very small, just one millionth of the neutron star's radius: about one centimeter! The neutron star's strong magnetic field could be another source of deformations. Simulations of these magnetic deformations show that they can induce (much) smaller ellipticities of up to 10-8, or about the width of a human hair.
What is a continuous gravitational wave and how does it differ from the signals observed so far?
All of the gravitational wave events observed so far by the Earth-based interferometric gravitational-wave detectors were emitted in the final orbits of black hole or neutron star pairs that were inspiralling and eventually merging. These events are transient: Depending on the masses involved, they are in the detectors' frequency range from a fraction of a second to about a minute before they end. Before and afterwards, no gravitational waves are observed.
Einstein@Home searches for a different kind of signal: The gravitational waves emitted by deformed spinning neutron stars are continuous – they are there at all times.
They are also much fainter (because of the much smaller masses involved) than the gravitational waves from merging black holes and neutron stars. We expect the strongest continuous gravitational waves to be at least a factor of 10,000 fainter than a “loud” binary black hole merger.
While this may seem like bad news, the continuous and fairly simple nature of the signal compensates for its faintness. By analyzing long (i.e. months) periods of data, even very weak signals can be detected. What's more: Once a possible signal is identified, it can be observed again and again. It will be there in the future, as better observations with more sensitive detectors become available and as analysis methods improve.
How do we search for continuous gravitational waves?
The gravitational wave emitted by a deformed spinning neutron star is very simple. It is almost perfectly monochromatic. This means that it has a single frequency (twice the rotation frequency of the neutron star). This instantaneous frequency decreases slowly over time as the spinning neutron star loses energy through the emission of gravitational (and, if it is a pulsar, electromagnetic) waves.
If one were to observe the gravitational-wave emission while floating in space at rest relative to the rotating deformed neutron star, things would be easy. Finding nearly monochromatic gravitational waves in a noisy detector is straightforward: A simple Fourier analysis would quickly reveal the periodicity.

But in reality, the actual search is much more complicated and computationally demanding. One of the main reasons: Our detectors are not at rest relative to the neutron star. They sit on the surface of the Earth, which rotates daily and orbits the Sun once a year: The detectors are moving relative to the neutron star. This causes a Doppler shift in the gravitational-wave frequency observed by the detectors. The strength of the Doppler effect depends on time (during a day and within a year) and on the position of the neutron star in the sky. The plot on the right shows a simulation of a continuous gravitational-wave signal received on Earth. You can observe the annual and daily Doppler effect modulations.
To describe a continuous gravitational-wave signal, four different parameters are required: the sky position (two parameters, for example: right ascension and declination), the gravitational-wave frequency (one parameter), and the change of the gravitational-wave frequency over time (one parameter, usually called spin-down).
To search for a faint signal in noisy detector data, long stretches of data (covering months of observations) must be analyzed. If the parameters of the signal are unknown, many different possible parameter combinations must be tested: Suppose there's a signal with a certain frequency, spin-down, and position in the sky. This combination of parameters will tell you what the expected signal would look like. Now, check the detector data for the presence of the expected signal using Fourier analysis methods. If nothing is found, try again with a different combination of parameters.
Such a search requires a very large number of parameter combinations. This is because, over time, even a tiny offset in one of the parameters would cause the search to potentially miss a signal hidden in the detector noise: Assume a frequency value just a little off from the true one, and the signal will not show up in the analysis. The same holds for offsets in sky position or spin-down. To minimize the chance of missing a hidden signal, the data is very finely combed using a large number of parameter combinations.
Learn more about the search for continuous gravitational waves in this video hosted on YouTube.
What data does Einstein@Home analyze?
In its search for gravitational waves, Einstein@Home analyzes public data from previous observing runs of the LIGO detectors, available through the Gravitational Wave Open Science Center. These data sets typically span several months and may be interrupted by shorter or longer pauses, such as for detector maintenance.
On these data sets, Einstein@Home performs different types of searches, varying in the amount of a priori information and the number of unknown signal parameters.
What is an all-sky search?
In a typical Einstein@Home all-sky search, none of the four signal parameters (sky position, frequency, and frequency change) are known a priori. We search for signals from all possible sky positions and over a wide range of frequencies and frequency changes. Because there is little prior information, the most sensitive search possible, using all available data in one long stretch, isn't computationally feasible. It would require far more computing power than is available.
The next best thing is a hierarchical search, which divides the data into smaller consecutive segments. Each of these segments is analyzed independently in an optimal way. Then, the results from the individual segments are combined in a clever way. The end result is a search that is almost as sensitive as the optimal one – at far less computational cost. But even with this trick, large computer clusters or volunteer computing projects like Einstein@Home are needed to perform these searches.
What is a directed search?

In certain cases, some information about the potential sources of continuous gravitational waves will be available a priori. For known supernova remnants, the position of the central neutron star is known from observations in the electromagnetic spectrum. Therefore, the position in the sky is precisely determined and does not need to be searched. Even if the position is not precisely known, it can be constrained to a very small patch of sky. That leaves only two unknowns: The gravitational-wave frequency and its evolution over time.
In these directed searches, only the unknown frequency, its change, and possibly a few sky positions need to be searched. For example, Einstein@Home has searched for gravitational waves from central compact objects in the supernova remnants Vela Jr., Cassiopeia A (see image on the right), and G347.3.
What have we learned so far?
So far, no continuous gravitational wave signal has been observed. But the searches have already provided insights into the hidden population of neutron stars in our Galaxy.
Einstein@Home is conducting the most sensitive all-sky searches for continuous gravitational waves in LIGO data. The results of these searches constrain the Galactic neutron star population by excluding the presence of rapidly rotating deformed neutron stars close within hundreds of light-years around Earth: If these objects existed, the Einstein@Home analyses would have detected their continuous gravitational waves by now.
Other targeted searches for gravitational waves from central compact objects in supernova remnants constrain the deformation of these young neutron stars. The Einstein@Home results provide the strongest constraints known to date.
A complete list of all Einstein@Home result publications is available at our Publications page.
What do we expect to learn in the future?
The first detection of continuous gravitational waves will be our first glimpse of the vast, so far hidden population of neutron stars in our home galaxy. We estimate that there are about 100 million neutron stars in the Milky Way, of which we currently know about 3500 because they have been observed as pulsars. Gravitational waves will provide an entirely new way to probe the dark, unseen majority of this neutron star population.
Observing continuous gravitational waves could also shed light on the unkown internal structure of neutron stars, could allow us to study the behavior of matter under extreme conditions and improve our understanding of stellar evolution and stellar populations.
The LIGO detectors will become even more sensitive in the near future, producing more data that Einstein@Home can analyze. This will allow us to look deeper into our Galaxy: We will be able to search for more distant or less deformed neutron stars.
What happens when your computer discovers a gravitational wave?
If the analysis of a particular set of workunits looks promising and shows clear or faint signs of a continuous gravitational wave, further follow-up analyses of gravitational-wave detector data are conducted to confirm the astrophysical origin of the gravitational-wave candidate.
The handful of users, on whose computers the initial data analysis was performed that found the candidate with the highest significance, will be credited in the acknowledgements section of the scientific discovery paper. They will also receive personalised framed discovery certificates, which also show information on the gravitational wave that their computer found. They might also become part of the media coverage about the discovery.
Copyright © 2024 Einstein@Home. All rights reserved.
